By utilizing more complex magnet geometries, a high temperature plasma can be confined without any internal currents.
Image Carousel with 4 slides
A carousel is a rotating set of images. Use the previous and next buttons to change the displayed slide
-
Slide 1: Magnetic fields in the on-campus Columbia Stellarator
-
Slide 2: The Wendelstein 7-X Stellarator Project in Germany
-
Slide 3: Calculated instability structure in the Columbia stellarator
-
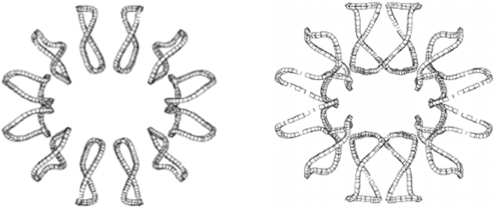
Slide 4: Example stellarator coil geometries designed by Columbia researchers
Columbia researchers, in particular Professor Allen Boozer, pioneered the development of Stellarator configurations that have a superior ability to retain heat in the plasma. Advances by Columbia researchers enabled projects such as the pictured Wendelstein 7-X facility in Germany to achieve performance far above previous designs. Please expand the links below to explore active work in this area.
Stellarator Theory
The stellarator configuration is an alternate fusion reactor concept in which complex three-dimensional (3D) electromagnets confine a high performance plasmas. As compared to a tokamak configuration, the stellarator is inherently more controllable and is much more stable to current-driven instabilities. These improved physics properties come with a cost of increased complexity, owing to the highly 3D geometries that must be designed around.
Columbia researchers, led by Prof. Allen Boozer, have developed theoretical techniques that enable definition of the complex plasma and magnet geometries that enable high performance. All modern stellarator research is done in a special coordinate system, called `Boozer Coordinates’, where hidden stellarator symmetry properties are automatically enforced. This work has enabled the next generation of stellarator projects (such as the Wendelstein 7-X, pictured above) to be designed and constructed. More recently Prof. Boozer is engaged in advocating for a strong stellarator research program in the United States, and continuing to design advanced stellarator configurations with symmetry and performance properties that are needed in a stellarator fusion reactor.
Dr. Elizabeth Paul uses theoretical and computational methods to study the magnetic confinement of plasmas in stellarators. Dr. Paul’s research integrates applied mathematical techniques to improve the design of stellarator configurations through numerical optimization. She studies the rich behavior present in three-dimensional magnetic confinement devices, including the nonlinear dynamics of fast particle populations.